One Zillion Bucks
Author:
Michael Asper
Last Updated:
před 10 lety
License:
Creative Commons CC BY 4.0
Abstract:
Zeta functions :-)

\begin
Discover why over 20 million people worldwide trust Overleaf with their work.
Zeta functions :-)

\begin
Discover why over 20 million people worldwide trust Overleaf with their work.
\documentclass[a4paper, 12pt]{article}
\usepackage{geometry}
\geometry{margin=1in}
\usepackage[english]{babel}
\usepackage[utf8]{inputenc}
\usepackage{amsmath}
\usepackage{commath}
\usepackage{amsthm}
\usepackage{amssymb}
\usepackage{setspace}
\usepackage{units}
\usepackage{graphicx}
\doublespacing
\title{One Zillion Bucks}
\newtheorem{theorem}{Theorem}[section]
\newtheorem{lemma}[theorem]{Lemma}
\begin{document}
\begin{center}
One $\zeta$illion Bucks
\end{center}
\begin{center}
Michael Asper \quad
Chris Charnecki
\end{center}
\begin{center}
Mason Forshage \quad
Becca Landman
\end{center}
\paragraph{} In the world of mathematics, there exists a list of seemingly unsolvable problems, each with a prize of one million dollars for their completion. They are called the Millennium Prize Problems. One such problem is to prove the Riemann Hypothesis conjecture, which involves a type of $\zeta$-functions. It states that all non-trivial zeros of the so-called Riemann $\zeta$-function all possess the real part $\nicefrac{1}{2}$.
\paragraph{} To elaborate upon the $\zeta$-functions and non-trivial zero, $\zeta$-functions exist as functions whose arguments can only be complex; however, there exist a singularity pole at 1. The $\zeta$-function possesses zeros at the negative even integers e.g. $\zeta$(-2),$\zeta$(-4),$\zeta$(-6), $\ldots$. These solutions are considered to be trivial as opposed to the "non-trivial" solution which exist on the aptly-named “critical line” represented by the complex numbers with the form,
\begin{equation}
\frac{1}{2} + yi, \quad y\exists \mathbb{R}
\end{equation}
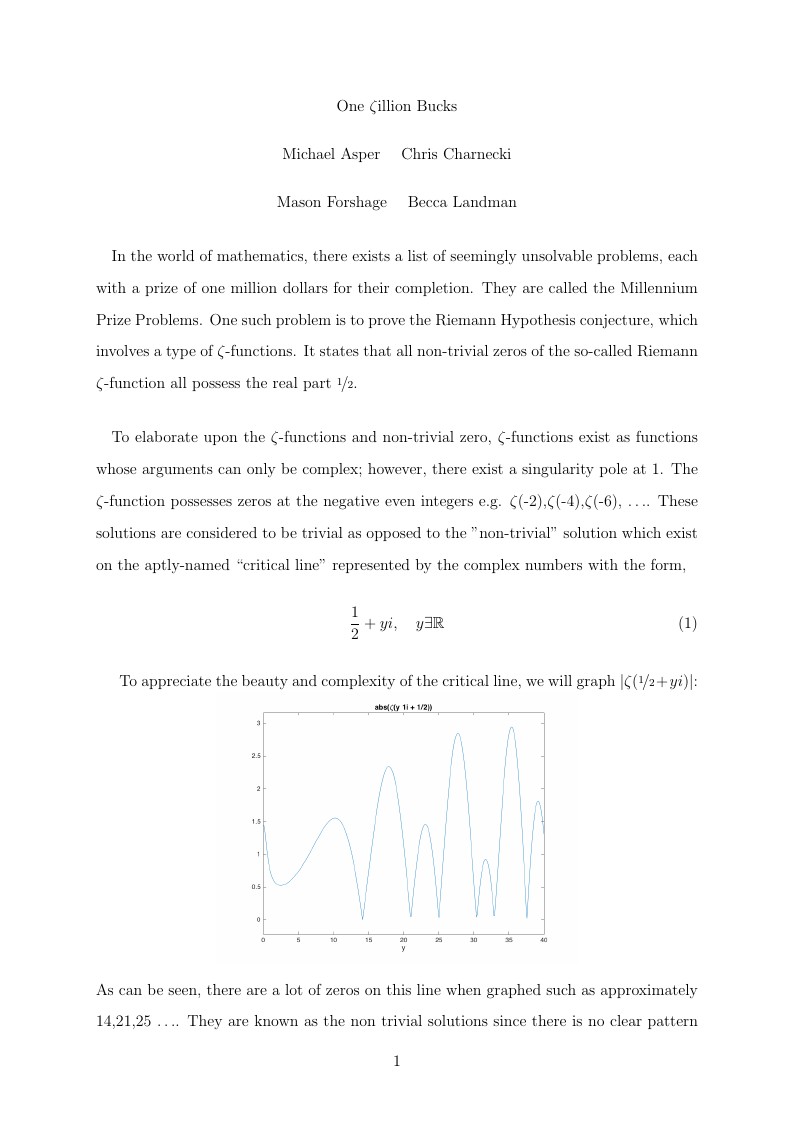
To appreciate the beauty and complexity of the critical line, we will graph \(|\zeta(\nicefrac{1}{2} + yi)| \):
\newline
\centerline{\includegraphics[width=0.6\textwidth]{crit.png}}
As can be seen, there are a lot of zeros on this line when graphed such as approximately 14,21,25 $\ldots$. They are known as the non trivial solutions since there is no clear pattern otherwise called \textit{zeros of the zeta function}. The Riemann Hypothesis is all about the zeros of the function.
\paragraph{Definitions} Throughout the proof, we will be using a lot of equations that are beyond the scope of this proof, so therefore will be defined ahead of time in order to simplify the paper.
$\zeta$-Function:
\begin{equation}
\zeta(s) = \sum^{\infty}_{n=1} \frac{1}{n^s} = \frac{1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \ldots \quad s = x + yi \quad \mathbb{R}(x) > 1
\end{equation}
Jacobi Theta Function:
\begin{equation}
\sum^{\infty}_{n=1} e^{-\pi n^2x} dx = \psi(x) dx.
\end{equation}
Simplified Integrals:
\begin{equation}
\int^{\infty}_{0} x^{\frac{s}{2}-1} \psi(x) dx = \int^{\infty}_{1} \left(x^{\frac{s}{2}} + x^{\frac{1-s}{2}} \right) \frac{\psi(x)}{x}dx - \frac{1}{s(1-s)}
\end{equation}
Several definitions of $\Gamma$-functions:
\begin{equation}
\Gamma(s) = (s-1)!
\end{equation}
\begin{equation}
\Gamma(2s) = \frac{{2}^{2s-1}}{\sqrt[]{\pi}}\Gamma(s) \Gamma \left(s + \frac{1}{2}\right)
\end{equation}
\begin{equation}
\Gamma(s)\Gamma(1-s) = \frac{\pi}{\sin(\pi s)}.
\end{equation}
\begin{equation}
\Gamma(s) = \int^{\infty}_{0} t^{s-1} e^{-t} dt.
\end{equation}
\begin{proof}
We will show $\zeta$(2) = $\nicefrac{\pi^2}{6}$. When we try to the find sum of the series,
\begin{equation}
S_{2} = \zeta(2) = \sum^{\infty}_{n=1} \frac{1}{n^2},
\end{equation}
we would typically use an improper integral method to evaluate a series of this form, which would be shown as,
\begin{equation}
\int^{\infty}_{1} \frac{1}{x^2} dx = \lim_{t \rightarrow \infty} \int^{t}_{1} \frac{1}{x^2} dx
\end{equation}
\begin{equation}
\lim_{t \rightarrow \infty} -\frac{1}{x} \biggm|^{t}_{1}
\end{equation}
\begin{equation}
\lim_{t \rightarrow \infty} -\frac{1}{t} + \frac{1}{1} = 1
\end{equation}
However, using Taylor series, we will show that this is not true when trying to find the sum of the series, \(S_{2}\). That is because the integral is only an indicator of convergence and not the actual value of the sum. Let us write the Taylor series for \(\sin(x)\),
\begin{equation}
\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} \pm \ldots
\end{equation}
We will divide the series by \(x\) for later manipulation.\footnote{The authors will note that this type of proof usually requires using a factorization theorem such as Weierstrass factorization theorem or Hadamard factorization theorem. We will avoid using such methods, but for a deeper understanding and a more rigorous proof, the reader can research more into those methods.}
\begin{equation}
\frac{\sin(x)}{x} = 1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} \pm \ldots \quad x \neq 0
\end{equation}
Now we must find the roots of the equation. This means we will find anytime $\sin(x)$ is equal to 0. This occurs every time \(x\) is equal to \(\pm n\pi\). Therefore some of the roots are,
\begin{equation*}
\begin{aligned}
x=\pi \quad x = 2\pi \quad x = 3\pi \quad x = n\pi \\
x=-\pi \quad x = -2\pi \quad x = -3\pi \quad x = -n\pi
\end{aligned}
\end{equation*}
The next step is to actually rewrite these roots, and use it to represent the Taylor series function. In other words, just like how you can use the factored roots of a polynomial\footnote{$x^2 + 4x + 3 = (x+1)(x+3)$ is an example of representing a polynomial as its roots.} to represent the equation, we will do the same thing with the series function; however, we will also apply some manipulation to the roots. We will first divide both sides of \(x = n\pi \) by $n\pi$ obtaining,
\begin{equation}
\frac{x}{n\pi} = 1.
\end{equation}
Afterwards, we will move the \(x\)-variable to the left-side in order to set it equal to zero,
\begin{equation}
0 = 1 - \frac{x}{n\pi}.
\end{equation}
The authors will show how some of the roots will look,
\begin{equation*}
\begin{aligned}
0=1 - \frac{x}{\pi} \quad 0=1 - \frac{x}{2\pi} \quad 0=1 - \frac{x}{3\pi} \\
0=1 + \frac{x}{\pi} \quad 0=1 + \frac{1x}{2\pi} \quad 0=1 + \frac{x}{3\pi}
\end{aligned}
\end{equation*}
Now, we can represent the Taylor series function as its roots,
\begin{equation}
\frac{\sin(x)}{x} = \left(1 - \frac{x}{\pi} \right)\left(1 + \frac{x}{\pi} \right)\left(1 - \frac{x}{2\pi} \right)\left(1 + \frac{x}{2\pi} \right)\left(1 - \frac{x}{3\pi} \right)\left(1 + \frac{x}{3\pi} \right) \ldots
\end{equation}
We will distribute in pairs using a difference of squares to simplify the series,
\begin{equation}
\frac{\sin(x)}{x} = \left(1 - \frac{x^2}{\pi^2} \right)\left(1 - \frac{x^2}{4\pi^2} \right)\left(1 - \frac{x^2}{9\pi^2} \right) \ldots
\end{equation}
Here is where we will now start distributing all the terms. Essentially, we are distributing infinite many times, and then reorganizing the terms by their \(x\)-degree,
\begin{equation}
\frac{\sin(x)}{x} = 1 + \left(- \frac{x^2}{4\pi^2}- \frac{x^2}{9\pi^2}- \frac{x^2}{\pi^2}-\ldots\right)+\left(\frac{x^4}{2\pi} + \frac{x^4}{9\pi} + \frac{x^4}{36\pi} + \ldots\right)-\left(\frac{x^6}{36\pi}+\ldots\right)+\ldots
\end{equation}
For this proof and the sake of space, we will ignore all the powers of \(x\) greater than 2 since it is irrelevant at the moment for finding the solution,
\begin{equation}
\frac{\sin(x)}{x} = 1 + \left(- \frac{x^2}{4\pi^2}- \frac{x^2}{9\pi^2}- \frac{x^2}{\pi^2}-\ldots\right) + \ldots
\end{equation}
This is where things get really interesting. We will factor out a $-\nicefrac{x^2}{\pi^2}$ and focus solely on the second degree term,
\begin{equation}
-x^2 \left[\frac{1}{\pi^2} \left(1 + \frac{1}{4} + \frac{1}{9} + \ldots \right)\right].
\end{equation}
Finally, we can see the series of reciprocal squares in the equation and now can include the sum with a little manipulation to make sure the equality stays,
\begin{equation}
-x^2 \left[\frac{1}{\pi^2} \left(1 + \frac{1}{4} + \frac{1}{9} + \ldots \right)\right] = -\frac{x^2}{\pi^2} \sum^{\infty}_{n=1} \frac{1}{n^2}
\end{equation}
Refer back to the Taylor Series of $\frac{\sin(x)}{x}$(14), and look at the coefficient of the second-degree term. The coefficient is equal to $\nicefrac{1}{3!}$. Therefore the bracketed part in equation (21) and (22) must equal the same coefficient! The reason is because since all the roots are equal to the Taylor series, and that means since we have organized all the second-degree \(x\) terms for both equations, this means they have to equal the same thing since there is no other way to affect the value of the second degree \(x\) coefficient. We can substitute in the new coefficient, $\nicefrac{1}{3!}$,
\begin{equation}
-\frac{x^2}{3!} = -\frac{x^2}{\pi^2} \sum^{\infty}_{n=1} \frac{1}{n^2}.
\end{equation}
By algebraic manipulation and computation of the factorial, we will finally show,
\begin{equation}
\frac{\pi^2}{6} = \sum^{\infty}_{n=1} \frac{1}{n^2}.
\end{equation}
Ultimately, by referring back to (9), we see,
\begin{equation}
\zeta(2) = \sum^{\infty}_{n=1} \frac{1}{n^2}
\end{equation}
\begin{equation}
\zeta(2) = \frac{\pi^2}{6}.
\end{equation}
\end{proof}
\paragraph{Functional Equation}
The Riemann-$\zeta$ function is defined for real numbers greater than one; however, we can use a functional equation to transform the domain of the equation, enabling us to show that $\zeta$(-1) has a defined value, which was not previously in the domain.
\begin{proof} We will show that the $\zeta$-function can be expanded for values less than 1, by showing $\zeta$(-1) exists.
Let us start off by using one of the $\Gamma$-functions defined earlier,
\begin{equation}
\Gamma(s) = \int^{\infty}_{0} t^{s-1} e^{-t} dt.
\end{equation}
We will make substitutions for \(s\) and \(t\) in the integral,
\begin{equation}
s \rightarrow \frac{s}{2}:\Gamma\left(\frac{s}{2}\right)= \int^{\infty}_{0} t^{\frac{s}{2}-1} e^{-t} dt.
\end{equation}
\begin{equation}
Sub: t = \pi n^2 x \quad \rightarrow \quad dt = \pi n^2 dx
\end{equation}
\begin{equation}
\Gamma\left(\frac{s}{2}\right)= \int^{\infty}_{0} {\left(\pi n^2 x\right)}^{\frac{s}{2}-1}e^{-\pi n^2 x} \pi n^2 dx
\end{equation}
\begin{equation}
\Gamma\left(\frac{s}{2}\right)= \int^{\infty}_{0} {\pi}^{\frac{s}{2}} n^s {x}^{\frac{s}{2}-1}e^{-\pi n^2 x} dx
\end{equation}
We will rearrange around some terms,
\begin{equation}
{\pi}^{-\frac{s}{2}} {n}^{-s} \Gamma\left(\frac{s}{2}\right)= \int^{\infty}_{0} {x}^{\frac{s}{2}-1}e^{-\pi n^2 x} dx
\end{equation}
Sequentially, we will sum both sides from 1 to $\infty$,
\begin{equation}
\sum^{\infty}_{n=1}{\pi}^{-\frac{s}{2}} \Gamma\left(\frac{s}{2}\right){n}^{-s} =\sum^{\infty}_{n=1} \int^{\infty}_{0} {x}^{\frac{s}{2}-1}e^{-\pi n^2 x} dx.
\end{equation}
Afterwards, we will rearrange where the sum is,
\begin{equation}
{\pi}^{-\frac{s}{2}} \Gamma\left(\frac{s}{2}\right)\sum^{\infty}_{n=1}\frac{1}{n^s} =\int^{\infty}_{0} {x}^{\frac{s}{2}-1}\sum^{\infty}_{n=1}e^{-\pi n^2 x} dx.
\end{equation}
Next, using the Jacobi Theta function (which was defined in the definitions), we can make a direct substitute,
\begin{equation}
{\pi}^{-\frac{s}{2}} \Gamma\left(\frac{s}{2}\right)\sum^{\infty}_{n=1}\frac{1}{n^s} = \int^{\infty}_{0} x^{\frac{s}{2}-1} \psi(x) dx.
\end{equation}
For ease, the simplified version of the integral was defined earlier in equation (4) to compute part of the integral and save time for us, and then we will also substitute in the $\zeta$-function as defined earlier,
\begin{equation}
{\pi}^{-\frac{s}{2}} \Gamma\left(\frac{s}{2}\right)\zeta(s) =\int^{\infty}_{1} \left(x^{\frac{s}{2}} + x^{\frac{1-s}{2}} \right) \frac{\psi(x)}{x}dx - \frac{1}{s(1-s)}.
\end{equation}
To complete the proof, we substitute in \(1-s\) for \(s\) and show that the right-hand side of the equation will equal the same thing,
\begin{equation}
Sub: s \rightarrow 1-s
\end{equation}
\begin{equation}
{\pi}^{-\frac{1-s}{2}} \Gamma\left(\frac{1-s}{2}\right)\zeta(1-s) =\int^{\infty}_{1} \left(x^{\frac{1-s}{2}} + x^{\frac{1-1+s}{2}} \right) \frac{\psi(x)}{x}dx - \frac{1}{1-s(1-1+s)}.
\end{equation}
\begin{equation}
{\pi}^{-\frac{1-s}{2}} \Gamma\left(\frac{1-s}{2}\right)\zeta(1-s) =\int^{\infty}_{1} \left(x^{\frac{s}{2}} + x^{\frac{1-s}{2}} \right) \frac{\psi(x)}{x}dx - \frac{1}{s(1-s)}.
\end{equation}
Looking at equation (39) and equation (36), we can state,
\begin{equation}
{\pi}^{-\frac{1-s}{2}} \Gamma\left(\frac{1-s}{2}\right)\zeta(1-s) = {\pi}^{-\frac{s}{2}} \Gamma\left(\frac{s}{2}\right)\zeta(s).
\end{equation}
We will now have to isolate the $\zeta$-function by itself. This requires us using some of the definitions of $\Gamma$-function defined earlier. We will start with equation (7),
\begin{equation}
\Gamma(s)\Gamma(1-s) = \frac{\pi}{\sin(\pi s)}.
\end{equation}
Afterwards, we will substitute in for $s$,
\begin{equation}
Sub: s \rightarrow \frac{s+1}{2} = \frac{s}{2}+\frac{1}{2}
\end{equation}
\begin{equation}
\Gamma \left( \frac{s+1}{2} \right)\Gamma \left(1- \frac{s+1}{2}\right) = \frac{\pi}{\sin(\frac{s\pi}{2}+\frac{\pi}{2})}.
\end{equation}
Since cosine is a co-function of sine by a shift of $\nicefrac{\pi}{2}$, we can use the co-function identity to replace the sine function,
\begin{equation}
\Gamma \left( \frac{s+1}{2} \right)\Gamma \left(1- \frac{s+1}{2}\right) = \frac{\pi}{\cos(\frac{s\pi}{2})}.
\end{equation}
Another definition of the $\Gamma$-function is (6),
\begin{equation}
\Gamma(2s) = \frac{{2}^{2s-1}}{\sqrt[]{\pi}}\Gamma(s) \Gamma \left(s + \frac{1}{2}\right)
\end{equation}
This also requires a substitution to get the $\Gamma$-function to match our $\zeta$ equations,
\begin{equation}
Sub: s \rightarrow \frac{s}{2} \quad \Gamma(s) = \frac{{2}^{s-1}}{\sqrt[]{\pi}}\Gamma\left(\frac{s}{2}\right) \Gamma \left(\frac{s+1}{2}\right)
\end{equation}
\begin{equation}
\frac{\sqrt[]{\pi}}{{2}^{s-1}}\Gamma(s) = \Gamma\left(\frac{s}{2}\right) \Gamma \left(\frac{s+1}{2}\right)
\end{equation}
Next, we will multiply both sides of (40) by $\Gamma\left(\frac{s+1}{2}\right)$
\begin{equation}
{\pi}^{-\frac{1-s}{2}}\Gamma\left(\frac{s+1}{2}\right) \Gamma\left(\frac{1-s}{2}\right)\zeta(1-s) = {\pi}^{-\frac{s}{2}}\Gamma\left(\frac{s+1}{2}\right) \Gamma\left(\frac{s}{2}\right)\zeta(s).
\end{equation}
Here we can see why all the setup was required and now can substitute in equations (44) and (47),
\begin{equation}
{\pi}^{-\frac{1-s}{2}}\frac{\pi}{\cos(\frac{s\pi}{2})}.\zeta(1-s) = {\pi}^{-\frac{s}{2}}\frac{\sqrt[]{\pi}}{{2}^{s-1}}\Gamma(s)\zeta(s).
\end{equation}
Now we will rearrange the equation to isolate one of the $\zeta$-functions. We will have to isolate the side without the $\Gamma$-function as dividing out a $\Gamma$-function is more difficult. Since this is mostly just algebra, we will jump straight to the finished product,
\begin{equation}
\zeta(1-s) = \frac{2}{(2\pi)^s} \cos\left(\frac{\pi s}{2}\right)\Gamma(s)\zeta(s)
\end{equation}
Finally, we set \(s\) equal to 2,
\begin{equation}
\zeta(1-2) = \frac{2}{(2\pi)^2} \cos\left(\frac{2\pi}{2}\right)\Gamma(2)\zeta(2)
\end{equation}
We will need to know $\zeta(2)$ is equal to $\nicefrac{\pi^2}{6}$, which was shown in the first proof,
\begin{equation}
\zeta(-1) = \frac{2}{4\pi^2} \cos\left(\frac{2\pi}{2}\right)(2-1)!\frac{\pi^2}{6}
\end{equation}
\begin{equation}
\zeta(-1) = \frac{1}{2} (-1)(1)\frac{1}{6}
\end{equation}
\begin{equation}
\zeta(-1) = -\frac{1}{12}
\end{equation}
Now to "connect" with the summation of all natural numbers by using the definition from equation (2) and therefore proving that $\zeta$(-1) exists, which shows the function can be extended allowing the existence of the critical line,
\begin{equation}
\zeta(-1) = \sum^{\infty}_{n=1}\frac{1}{{n}^{-1}}= \frac{1}{1^{-1}} + \frac{1}{2^{-1}} +\frac{1}{3^{-1}} +\frac{1}{4^{-1}} + \ldots = 1 + 2 + 3 + 4 + \ldots = -\frac{1}{12}
\end{equation}
\end{proof}
\paragraph{Conclusion:} As mentioned at the start of this paper, one application of $\zeta$-functions is the ability to prove the Riemann Hypothesis conjecture. This was introduced by Bernhard Riemann in 1859\cite{ref2} and when proved, would give invaluable insight into the field and distribution of prime numbers. Prime numbers are an important piece of math as they are \textit{literally} the foundation of all other numbers (as can be seen through prime factorization). Riemann’s conjecture uses $\zeta$-functions and the zeros of the function as the basis of his work. In short, we know how to find the value for any complex value in the $\zeta$-function except for \(x=1\) as that is a pole in the function; however, the most important values of the ones that get us zeros.
\paragraph{} Approximately the first \(10^{13}\)\cite{ref3} zeros have been found on the critical line, yet no one has been able to prove that all the zeros of the $\zeta$-function are \textbf{only} on the critical line. The conjecture itself holds implications for the distribution of prime numbers, and as such, if proved, would be unfortunate for computer security world-wide due to encryption algorithms' tendency to rely on prime numbers. Essentially since the Riemann Hypothesis is \textit{assumed} to be true by most mathematicians and cryptographers, it is already being used in cryptography; however, if proved, could show insight on prime numbers that would lead to better algorithms in finding primes or if the Riemann Hypothesis was actually \textit{disproved}, it might have an everlasting impacting on encryption since more cryptographers wouldn't have been able to know of other methods in determining primes. Because of this, it could be considered one of the most applicable conjecture in modern-day theoretical mathematics.
\paragraph{} Riemann Hypothesis is also connected to a lot of fields in mathematics and physics that scientists do not understand fully and is essentially helping bring fundamentals to. One example in physics is that the energy values of heavy nuclei such as Uranium and similar elements are distributed like the zeros in the Riemann $\zeta$-function. This implies there is a natural connection between prime numbers and quantum mechanics of heavy nuclei. Another application is in finance, where the zeros in the function are connected to random matrices in matrix theory that lets us model financial markets!
\paragraph{} Since this function has been so elusive for many years, numerous mathematicians are clamoring to solve it. If anyone is able to solve the conjecture at the line \(x=\nicefrac{1}{2}\), and prove that it works in a general case (or disprove it), they would be rewarded one million dollars and possibly earn much more throughout their lifespan.
\begin{thebibliography}{9}
\bibitem{ref1}
Davis, Harry F. (May 1989). Fourier Series and Orthogonal Functions. Dover
\bibitem{ref2}
Riemann, Bernhard (1859), "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse", Monatsberichte der Berliner Akademie.
\bibitem{ref3}
Weisstein, Eric W. "Riemann Zeta Function Zeros." From MathWorld
\end{thebibliography}
\end{document}